1. 　　　　　　　　　　　　　 　　(　 )

A. 2　　　　　　 　　　B. 　　　　　　　　C. 4　　　　　　　　 　D.

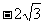
13. 解: (1) 設(shè)等比數(shù)列的公比為q, 則 ∴或,

∵的各項均為正數(shù), ∴. 所以.

(2) 由得. 數(shù)列是等差數(shù)列, ,

而

∵

∴當(dāng)時, . 　∴當(dāng)時, .

12. (1)

(2) 設(shè)抽去是第k項則有: ,

移項得:

,

所以抽去的是79,

11. 解: (1) 由得

由, 得

又, 所以

∴ 數(shù)列的通項公式為;

(2)由(1)可知是首項為, 公比為項數(shù)為n的等比數(shù)列,

∴

7. ;　　 　8. 　　　　9. 　2　 , 　　8　 ;　　　 　10. 　10　 .

(二) 專題測試與練習(xí)

(一) 典型例題

例1. 解：故

例2. 解：(1) ,

所以,

(2) 　所以

同理……,

所以

由此得 于是

的通項公式為:

當(dāng)n為奇數(shù)時, 　當(dāng)n為偶數(shù)時,

例3. 解：(1) 或.

取.

(2)

假設(shè)存在, 則有

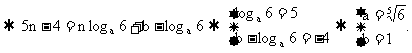
存在, 使成立.

11. 數(shù)列的前n項和為, 且, 求

　 (1) ,,的值及數(shù)列的通項公式;　 　(2) 的值.

12. 有窮數(shù)列的前n項和S _n＝2n²+n, 現(xiàn)從中抽取某一項(不是首項和末項)后, 余下項的

平均值是79.　 (1)求數(shù)列的通項;　 (2)求數(shù)列的項數(shù)及抽取的項數(shù).

13. 已知等比數(shù)列共有m項, 且各項均為正數(shù), , ++.

(1) 求數(shù)列的通項;

(2) 若數(shù)列是等差數(shù)列, 且, , 判斷數(shù)列前m項的和與數(shù)列的前m項和的大小并加以證明.

數(shù)列的綜合運用解答

10. 在各項均為正數(shù)的等比數(shù)列中, 若則

　　　　　　　　 .

9. 已知一個等比數(shù)列首項為1, 項數(shù)是偶數(shù), 其奇數(shù)項之和為85, 偶數(shù)項之和為170, 求這個

數(shù)列的公比　　 　　　　　, 項數(shù)為　 　　　　　　.