2．不共面的四個定點到平面的距離都相等，這樣的平面共有　　 ( D )

A．3個　 　　　　　　　　　 B．4個　　 　　　　　　　　 C．6個 　　　　　　　　　　　 D．7個

1．在棱長為a的正方體ABCD－A₁B₁C₁D₁中，與BC成異面直線且距離等于a的棱有(　 )

A．3條　　　　　 　　　 B．4條　　　　 　　　　　 C．6條　　　　 　　　　 D．7條

12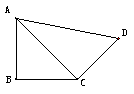．在平面四邊形ABCD中，已知AB=BC=CD=a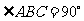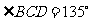，，，沿AC將四邊形折成直二面角B-AC-D，

(1)求證：面ABC⊥面BCD；

(2)求面ABD與面ACD所成的角。

解：(1)∵AB=BC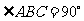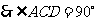，，，即AC⊥CD，

又面ABC⊥面ACD，交線為AC，∴CD⊥面ABC，∴面ABC⊥面BCD。

(2)過B作BE⊥AC于E，過E作EF⊥AD于F，

∵面ABC⊥面ACD，AC為交線，

又∵BE⊥AC，∴BE⊥面ACD，∴EF為BF在平面ACD內的射影，

又∵EF⊥AD，∴AD⊥BF，∴∠BFE為二面角B-AD-C的平面角。

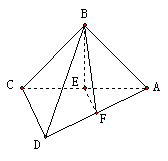∵AB=BC，BE⊥AC，∴E是AC的中點，∴，

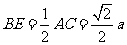又，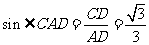

∴，

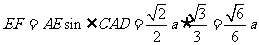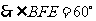，即為所求。

考查異面直線所成的角、直線與平面所成的角、平面與平面所成的二面角．要求掌握斜線在平面上的射影、直線與平面所成的角、二面角、二面角的平面角

理清求空間的角方法:一般是化歸為求兩條相交直線的夾角．通常應用“線線角抓平移，線面角抓射影，面面角抓平面角”而達到化歸目的．注意空間的角的計算應由“作、證、算”三個部分組成．首先應作出必要的輔助平面或輔助線；然后通過推理、論證找到某角就是所求的角；最后才是計算．

對于折疊問題, 要注意線的長度、角的大小及線線關系的變與不變。

11．已知四棱錐P-ABCD的底面為直角梯形，AB∥DC，底面ABCD，且PA=AD=DC=AB=1，M是PB的中點。

(1)求AC與PB所成的角；

(2)求面AMC與面BMC所成二面角的大小。

解：(1)過點B作BE//CA，且BE=CA，則

∠PBE是AC與PB所成的角．

連結AE，可知AC=CB=BE=AE=，又AB=2，所以四邊形ACBE為正方形．

由PA⊥面ABCD得∠PEB=90°,在Rt△PEB中BE=，PB=，

(2)作AN⊥CM，垂足為N，連結BN．在Rt△PAB中，AM=MB，

又AC=CB，∴△AMC≌△BMC,∴BN⊥CM，

故∠ANB為所求二面角的平面角．

∵CB⊥AC，由三垂線定理，得CB⊥PC，在Rt△PCB中，CM=MB，所以CM=AM．

在等腰三角形AMC中，AN·MC=，

．

∴AB=2,,

故所求的二面角為

10．如圖，在四棱錐P-ABCD中，底面為直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD，且PA＝AD=AB=2BC,M、N分別為PC、PB的中點．

(1)求證：PB⊥DM;

(2)求CD與平面ADMN所成的角

解：(1)因為是的中點，，所以．

因為平面，所以，從而平面．

因為平面，所以．

(2)取的中點，連結、，則，

所以與平面所成的角和與平面所成的角相等．

因為平面，所以是與平面所成的角．

在中，．

故與平面所成的角是．

9．在正四棱錐P-ABCD中，若側面與底面所成二面角的大小為60°，則異面直線PA與BC所成角的大小等于_____________．(結果用反三角函數值表示)arctan2

8．四面體ABCD中，E、F分別是AC、BD的中點，若CD=2AB=2，EF⊥AB，則EF與CD所成的角等于_____________．30°

7．已知二面角的大小為，為異面直線，且，則所成的角為　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　 B　 )

A．　　　　　 　　 B．　　　　 　　　　 C．　　　　　 　　　 D．

6．二面角內有一點P，若P到平面的距離分別是5,8，且P在平面的內的射影間的距離為7，則二面角的度數是　　　　　　　　　　　　 (　 C　 )

A．30⁰　　　　　　 　 B．60⁰　　　　　 　　　 C．120⁰　　　　　 　　 D．150⁰

5．如圖，平面α⊥平面β，A∈α，B∈β，AB與兩平面α、β所成的角分別為和，過A、B分別作兩平面交線的垂線，垂足為A′、B′，則AB∶A′B′＝　　　　　　 (　 A　 )

A．2∶1　　 　　　　　　　 B．3∶1　　 　　　　　　　　 C．3∶2　　　 　　　　　　 D．4∶3