
┐Ų─┐Ż║ üĒį┤Ż║ Ņ}ą═Ż║ĮŌ┤Ņ}
| 1̛ | 2̛ | 3̛ | 4̛ | 5̛ | |
| ╝ūĮM | 4 | 5 | 7 | 9 | 10 |
| ęęĮM | 5 | 6 | 7 | 8 | 9 |
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║ üĒį┤Ż║ Ņ}ą═Ż║ĮŌ┤Ņ}
| Ž▓Üg│į└▒ | ▓╗Ž▓Üg│į└▒ | ║Žėŗ | |
| ─ą╔· | 40 | 10 | 50 |
| ┼«╔· | 20 | 30 | 50 |
| ║Žėŗ | 60 | 40 | 100 |
| pŻ©K2Ī▌kŻ® | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║ üĒį┤Ż║ Ņ}ą═Ż║ĮŌ┤Ņ}
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║ üĒį┤Ż║ Ņ}ą═Ż║ĮŌ┤Ņ}
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║ üĒį┤Ż║ Ņ}ą═Ż║╠Ņ┐šŅ}
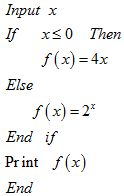
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║ üĒį┤Ż║ Ņ}ą═Ż║╠Ņ┐šŅ}
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║ üĒį┤Ż║ Ņ}ą═Ż║╠Ņ┐šŅ}
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║ üĒį┤Ż║ Ņ}ą═Ż║▀xō±Ņ}
| AŻ« | $\frac{{\sqrt{3}}}{3}$ | BŻ« | $\frac{{4\sqrt{3}}}{3}$ | CŻ« | $\frac{{8\sqrt{3}}}{3}$ | DŻ« | $\frac{{2\sqrt{3}}}{3}$ |
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║ üĒį┤Ż║ Ņ}ą═Ż║▀xō±Ņ}
| AŻ« | $-\frac{3}{5}$ | BŻ« | $-\frac{6}{5}$ | CŻ« | $\frac{6}{5}$ | DŻ« | $\frac{3}{5}$ |
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║ üĒį┤Ż║ Ņ}ą═Ż║▀xō±Ņ}
| AŻ« | $\frac{5}{8}$ | BŻ« | $\frac{5}{16}$ | CŻ« | $\frac{4}{7}$ | DŻ« | $\frac{5}{14}$ |
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
░┘Č╚ų┬ą┼ - ŠÜ┴Ģāį┴ą▒Ē - įćŅ}┴ą▒Ē
║■▒▒╩Ī╗ź┬ō(li©ón)ŠW(w©Żng)▀`Ę©║═▓╗┴╝ą┼Žó┼eł¾ŲĮ┼_ | ŠW(w©Żng)╔Žėą║”ą┼Žó┼eł¾īŻģ^(q©▒) | ļŖą┼įp“_┼eł¾īŻģ^(q©▒) | ╔µÜv╩Ę╠ō¤oų„┴xėą║”ą┼Žó┼eł¾īŻģ^(q©▒) | ╔µŲ¾ŪųÖÓ┼eł¾īŻģ^(q©▒)
▀`Ę©║═▓╗┴╝ą┼Žó┼eł¾ļŖįÆŻ║027-86699610 ┼eł¾Ó]ŽõŻ║58377363@163.com