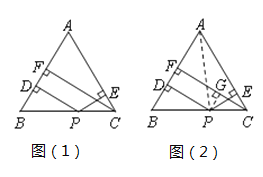
【題目】張老師給愛好學習的的小軍和小俊提出這樣一個問題:如圖(1)�,在△ABC中,AB=AC���,點P為邊BC上的任一點���,過點P作PD⊥AB,PE⊥AC����,垂足分別為D�,E,過點C作CF⊥AB��,垂足為F.求證:PD+PE=CF.
小軍的證明思路是:如圖(2)�,連接AP,由△ABP與△ACP面積之和等于△ABC的面積可以證得:PD+PE=CF.
老師表揚了小軍����,并且告訴小軍和小�����。涸谇蠼馄矫鎺缀螁栴}的時候���,根據(jù)有關(guān)幾何量與涉及的有關(guān)圖形面積之間的內(nèi)在聯(lián)系�����,用面積或面積之間的關(guān)系表示有關(guān)線段間的關(guān)系��,從而把要論證的線段之間的關(guān)系轉(zhuǎn)化為面積的關(guān)系����,并通過圖形面積的等積變換對所論問題來進行求解的方法����,這種方法稱為“面積法”.
請你使用“面積法”解決下列問題:
(1)Rt△ABC兩條直角邊長為3和4,則它的內(nèi)切圓半徑為 �����;
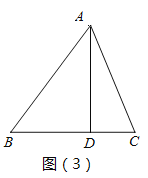
(2)如圖(3)�,△ABC中AB=15,BC=14,AC=13��,AD是BC邊上的高.求AD長及△ABC的內(nèi)切圓的半徑���;
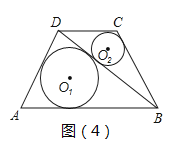
(3)如圖(4)����,在四邊形ABCD中���,⊙O1與⊙O2分別為△ABD與△BCD的內(nèi)切圓�,⊙O1與△ABD切點分別為E�、F、G��,設(shè)它們的半徑分別為r1和r2���,若∠ADB=90°�,AE=8�,BC+CD=20,S△DBC=36���,r2=2,求r1的值.